Introduction
首先,什么是因子?可以简单地认为是影响股票收益的、可分散化风险之外的系统性风险来源(或能解释股票风险溢价/回报率的变量);
当然最直观的因子就是市场因子,通常认为个股的风险溢价和市场的风险溢价是相关的(也就是说当大盘好的时候, 个股理应是上升的, 只是每个股票受大盘影响的程度各不相同)。
当我们确定了某个因子的影响力之后(因子的影响是整体的),结合个股的因子暴露,我们可以围绕因子和个股的因子暴露构建投资组合(portfolio);
每个股票对因子的暴露肯定是不同的,还是以市场因子为例,虽然大盘涨了,个股应该会涨, 但是不同类型的股票受影响程度是不同的, 比如银行股, 它对大盘的反映没有那么敏感, 也就是beta会小一些
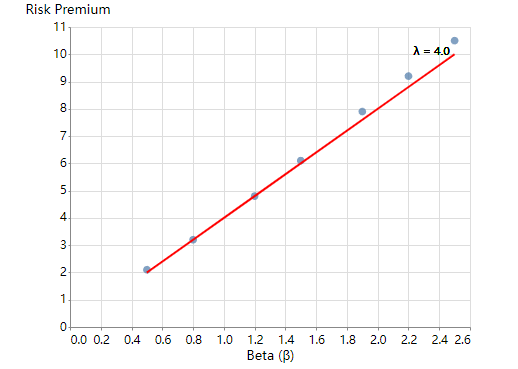
作为直观的演示,上面的回归的斜率就是因子的影响(因子风险溢价 λ),横轴上的 beta 是因子暴露,beta 和 lambda 共同决定了风险溢价(y 轴)的大小。
那么除了市场因子之外,还有哪些影响因子呢,或者说如何解释这些因子的影响呢,这个就是因子投资所关注的主题。
如何构建因子
首先我们需要解决 λ 是多少的问题,市场因子的风险溢价相对比较容易得到,就是整个市场的整体收益,当然我们可以调整这个整体收益的范围,比如可以去掉市值非常低的小盘股等等,甚至在实践中也可以使用类似沪深 300 等指数的超额收益率来代替。
但是其他因子的影响呢?比如公司的规模,我们可以直观地观察到小规模的公司风险溢价会比大型公司高,因为因子的影响是与个股无关的,所以可以很直觉地使用所有的小规模公司的平均风险溢价减去大规模公司的平均风险溢价来作为因子收益(影响力,也就是上面的 λ)的代理变量。
单一因子的情况下,我们只需要根据公司的规模进行单变量排序确定,根据排序的分位数,规模最小的 30%为小型公司(Small),规模最大的 30%为大型公司(Big),然后分别构建两个 portfolio,并计算它们之间的平均收益差值作为因子收益(λ)。
如何验证因子
当我们基于因子构建投资组合模拟了因子的收益率之后,该如何验证因子的有效性呢? 有两种主要的方法:
- 检验因子风险溢价:对因子收益率(T 期)进行 t 值统计,看这个因子的平均收益率是不是显著不等于 0(即是否存在风险溢价)。
- 检验因子 α:进行时间序列回归,看因子组合的超额收益是否能被现有已验证的因子模型(如 CAPM 或 Fama-French 三因子模型)所解释。具体来说,是将因子组合的超额收益对基准模型中的因子进行回归,检验回归的截距项 α是否显著不等于 0。如果 α 显著为 0,则表明该因子已被基准模型所解释,独立有效性较弱。
考虑到时间序列的自相关性,t 值通常需要进行 Newey-West 调整。
Fama-MacBeth 方法
业界还有一种评估因子有效性的方法,就是 Fama-MacBeth 方法(下面简称 FM 方法)。FM 方法是一种两步回归的方法:
- 首先进行横截面回归(cross-section regression, CSR)
Y(T 期的个股超额收益)~ X(期初的个股特征暴露,比如 β、市值、B/M)+ 截距项
FM并不需要构建 portfolio 来计算因子的收益,而是直接使用每个股票的属性,比如 B/M, 市值等作为因子的Beta(因子暴露);然后计算Beta的斜率(这个斜率可以模拟因子的效果)
2. 时序聚合
每一期通过横截面回归得到了T个Beta的斜率(coefficient), 然后就可以对每个Beta的斜率进行时序聚合,计算 t 值和 N-W 调整后的 t 值来验证这些斜率的有效性。如果这些斜率在统计上是显著的, 那么我们可以认为Beta对应的因子是有效的