第二章： B-Tree Basics

• B+ 树是几乎所有基于磁盘的关系型数据库(mysql， pg等)的基础数据结构
• B+ 树是Binary Search Tree的衍生， 有跟多的fanout, 所以搜索速度会更快（Log2 -> LogK, 当然在它们的算法复杂度是一致的）
• B+树的搜索见下图， 是从root根节点一直往下遍历的
• 数据的增删会触发B+数的split和merge（触发条件就是overflow和underflow）

示意图

B+树（n key， n+1 pointer结构， 当然有些B+树只会在叶子节点存储数据， 然后子节点之间用链表和双向链表来提升查询效率）.

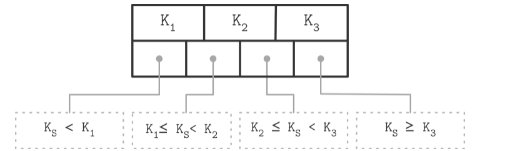
leaf node的split.

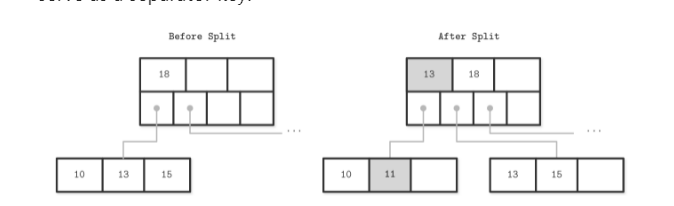
leaf node的merge

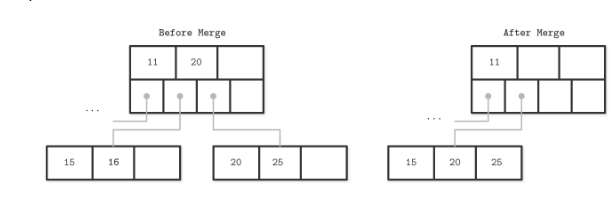
non-leaf node的split

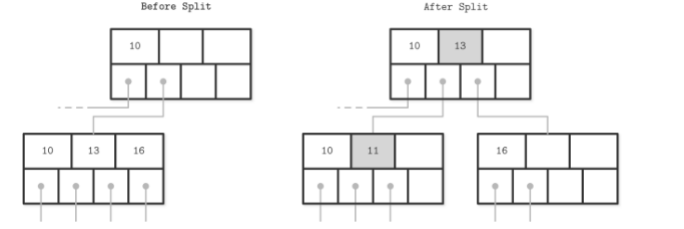
non-leaf node的merge

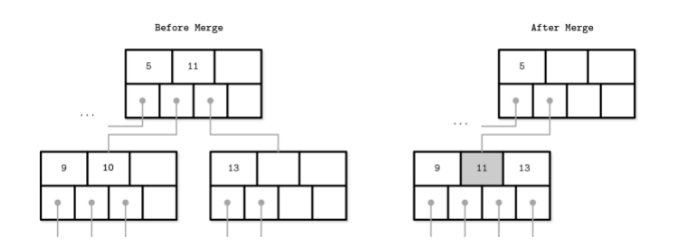
上面也看到了， 树的merge和split是比较耗时的操作(以split为例， 在某些场景下是需要一直向上递归的)， 特别在使用磁盘的场景下， 那么减少这种操作（调度）， 或者该表数据大小（压缩）通常会是优化数据库性能的重要方向

第三章 File Formats

基于磁盘存储的数据库， 它的主要的存储单元是Page, 大小一般是4kb-16kb之间， 基本上一个Page对应一个B-Tree的节点

原始的Page结构

• p： 指针， 指向子节点
• k: key
• v： value

这种结构非常适合用来存储大小固定的数据， 比如char(13)来存储电话号码(那么所有电话号码都是同样长度的， 这种方式的存储和查找非常的便利) 但是这种方式最大的问题是不好存储存储可变长度的数据， 比如string或者text

slotted page

现代数据库的page结构， 主要采用的是slotted page的形式：
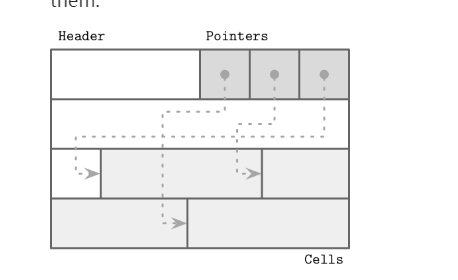
好处就是解决了原始Page结构不好存储可变长度记录的问题， 同时支持在数据被删除的时候进行更好的再利用（下面会提及）

Cell

cell存储各种类型的数据，它在Slotted Page中的插入方式是从尾部往前插入， 然后在Header中的Poitner会依次保留各个cell的offet信息

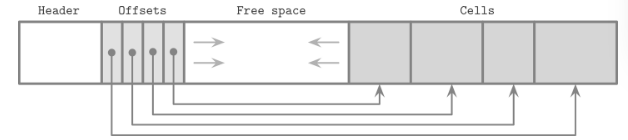
为什么采用这样的插入顺序其实也很好理解， 如果直接从左至右， 每次有一个新的cell, 那么原来存储在最左侧（紧挨着Header）的cell， 由于Header变化了， 它也需要相应地右移， 而从尾部向前则不需要

当然如果要保持Offset的逻辑顺序(比如根据Cell数据的字母序)， 我们可以调整Offset的位置

插入顺序： Tom -> Lesile -> Ron， Offsets的顺序则是Lesile -> Ron -> Tom

前面提到了， Slotted Page在空间再利用（reclaim space， 利用被删除的数据）的高效性， 以sqlite db为例， 数据库会维持一份可以用space的指针列表.
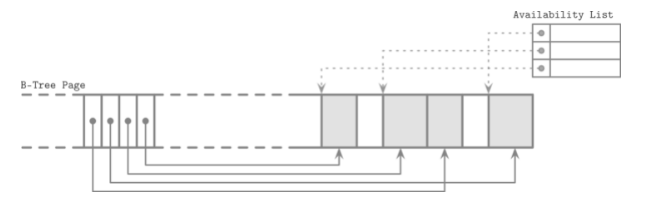
当要插入新的数据的时候， 会使用First fit或者Best fit算法去找到哪一块空间最最适合插入新数据

First fit: 找到第一块可以容纳新数据的space Best fit：找到浪费最小的space(就是space和新插入数据大小的差值最小) 从空间利用率上Best fit会更好，当然First fit速度明显会更快

假设， 没有办法找到任意一块能够容纳新数据的空白space， 并且我的空白space总和又大于新数据， 那这个时候就需要进行去碎片化(defragmenting)

Cell的结构

cell有两种， 第一种叫做Key Cell， 主要用来存储key。第二种是Key-Value Cell, 就是同时用来存储key和vlaue的， 一个page上面， 通常是这有这两种key中的任意一种的(因为两种key的结构略有不同， 所以从效率角度， 肯定是存储一种类型的会更好).

Key Cell结构：

• cell type
• key size
• child page id
• key bytes

Key-Value Cell结构:

• cell type
• key size
• value size
• key bytes
• Data record bytes(也就是value bytes)

第四章 Implementing B-Trees

Page Header

page header会存储一些和page相关的元信息， 除了上前面提到的cell offsets, 还会有诸如：

• Magic numbers
• sibling links
• rightmost pointers
• node high key

magic numbers是会存储在Page上的的特定位置的二进制的值， 比如存储第51 ， 47， 41， 45位的值， 目的是为了验证page有没有被污染， 只要在读数据的时候， 比较一下这几位的实际值和存储在header中的值是否一样即可 一般来说每个node， 会存储n个key以及n+1 pointer指向这个node的子节点， 这个第n个key经常会被存储在page header

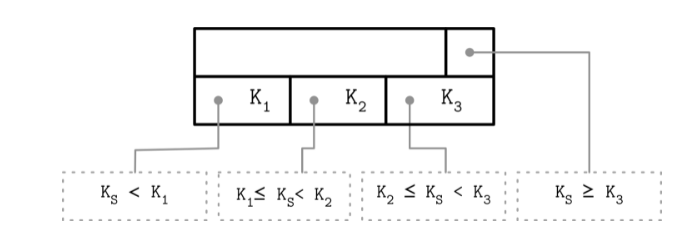
有时候， 这种方式会有一种变体就是key会饿pointer的数量对齐：
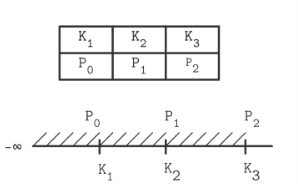
上面的K3就是high key

Overflow pages

通常page的size是固定的， 在4-16kb之间， 过大的size不可避免的会照成空间的浪费。 但是page size的固定话， 当可变长的数据过大的时候，我们就需要有一个扩展的页去存储溢出的数据, 这些页就被称为overflow page.

说到底， 磁盘的load reload的开销过大才需要固定size的page， 以及这种overflow page， 如果是内存， 之间原来的size 按比例扩容就好了

page header会保留指向这些overflow page的指针（overflow page也需要保留指向原始页面的指针）
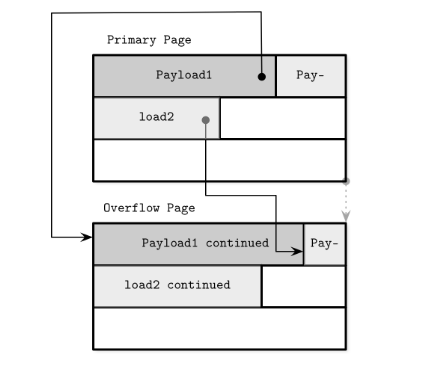
一般来说说， 一个page只会指向单一的overflow page， 如果还是放不下， 那么可以继续从overlow page出发链接新的overflow page

二分查找在页面中应用

由于page header中可以以逻辑顺序保留cell的offsets， 那么我们完全可以对这些offset进行二分查找：
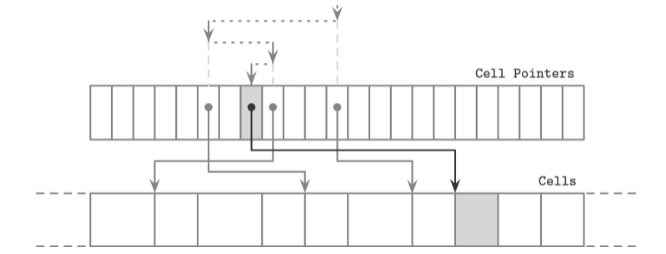
具体步骤就是， 现取这些offsets中最中间的那个， 然后找到对应的cell， 比较和查找键的大小来决定二分查找的方向是往左还是往右

页的Split和Merge的传播

随着数据的插入和删除， B树的节点需要进行相应的拆分 & 合并， 这意味着子节点的父节点以也会发生变化， 而且这种变化通常是一层层向上传播的。有没有一种高效的算法去更新这种变化 ， 其中一种就是Breadcrums（面包屑）， 这个算法的名称其实很形象地指出了它的实现方式： 我们查找新的插入节点， 一定是从根节点之上而下的， 如果我们记录了这个path的话， 那么将其逆序， 不就找到了每个子节点的父节点嘛？

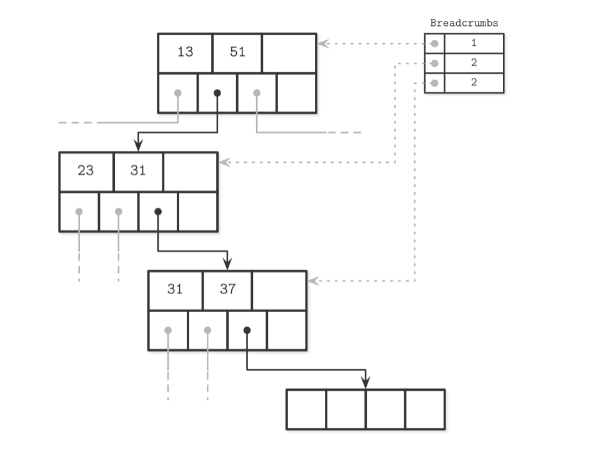
比如我们要插入一个大于37的数值， 查找路径入上入所示， Breadcrumbs记录了每个insertion point的offset。 Breadcumbs的实现一般是stack

Rebalancing

通常来讲， 树的再平衡会涉及到大量的split和merge， 进而影响数据库性能。所以数据库通常会延迟split和merge， 并使用一种相对开销较少的方式去实现reblancing – 平衡邻居节点之间的数据， 把有较多数据的节点的数据搬到隔壁的节点， 从而避免节点之间的split和merge

Right-only appends

很多场景下 ， 数据库都有一个自增的键比如一个自增的id， 如果还是采用常规的自上而下的查找方式是纯粹的浪费时间。 Postgresql等数据库， 会直接比较插入的key的值和最右页（存储最大数据的page）的第一个key进行比较， 如果查要插入的key的值更大且该页仍有足够空间， 那么就直接把数据插入到这个最右页上， 避免了自上而下的查找（计算复杂度变化： LogN -> 常数时间，改进很大），这种方式也叫fast path

压缩

数据的压缩会牵涉到一个很重要的指标： 压缩率:

• 更高的压缩率意味着更好的空间利用率
• 同时意味着， 更高的时间复杂度， 因为解压缩会消耗大量的cpu资源

很明显， 这里有一个非常重要的tradeoff : 空间vs时间

另外通常来讲， 我们不会再文件层级去压缩数据， 只会在page级别， 很明显前者会影响查询效率。

另外压缩的方式除了和page绑定在一起， 也可以作为一种插件的形式进行， 和page的管理进行解耦（比如对整个column的数据进行压缩， 其实列式数据就是这么做的）

第五章 Transaction Processing and Recovery

Buffer managment

类似于IO系统， 数据库也会使用类似缓存页(page cache)的概念来管理访问数据的缓存。

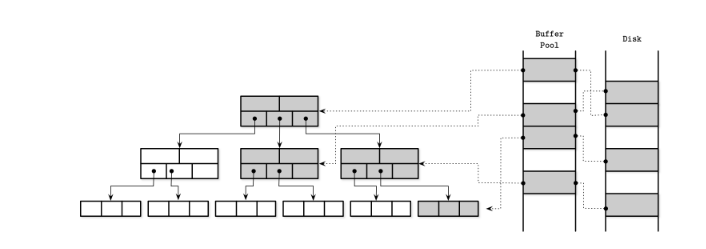
上图展示了B+树的节点Page在缓存池以及在磁盘上的对应关系。 Page cache机制的包括：

• 将数据保留在内存
• 如果要的Page在内存中， 直接返回缓存页
• 如果需要的Page不再内存中， 且Buffer pool足够大， 会将该页存储在缓存池（page in）
• 如果没有足够空间来存储新的缓存页， 就需要运行某种机制淘汰（eviction）一部分缓存页（比如使用LFU, LRU， CLOCK等算法）， 然后当缓存页被淘汰的时候， 会写道磁盘以保证数据的一致性

缓存页可以看作是数据请求和磁盘之间的中间层， 除了数据的读取， 数据的变更其实也是优先发生在这个中间层， 而不是直接写入到磁盘， 在内存中的缓存页数据被修改的时候， 这个时候这个页面就会被标识脏页(dirty page), 标识和磁盘数据不同步。 当然dirty page中的数据最后一定会被写入到磁盘， 为了保证这个过程不会出现纰漏（比如由于停电等原因， 改变的数据没有被同步到磁盘， 进而影响了数据库的ACID保证）， 通常会使用一种叫做WAL（write ahead log, 预写日志）的机制来保证数据的一致性

WAL其实就是一系列的数据变更记录， 通常会在事务成功发生之后（commit）被保存在磁盘， 由于很多条记录其实可以被合并成一条， 比如对一个账户A增加1000， 记录一次， 减少1000再记录一次， 那这两条记录就可以被抵消掉， 另外WAL虽然是基于磁盘的， 但是它是顺序写入而不是随机写入 ，所以它的写入速度也是很快的

缓存页淘汰机制

常见的有LRU（Least Recently Used）, LFU(Least Freaquntly Used)，CLOCK。 LRU会比较侧重一个时效性， 越是被最近访问的Page原容易被缓存（最新访问的page会被放到链表的尾部， 然后链表头部的数据会被淘汰掉）， 在实践中(不只是数据库领域)， LFU通常会更常用一点， LFU相较于LRU会更侧重Page的访问频率， 低频的页会被有限淘汰

Clock机制

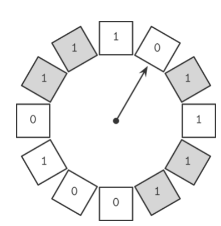
clcok机制就是用一种环形链表将所有的Page组织在一起， 当页面被访问， 它就会被设置为1（上图灰色所示）， 当后台运行淘汰任务的时候， ‘指针’随机指向一个Page, 如果它是0（最近没有被访问）就会被淘汰掉， 也就是说它和LRU相比， 增加了一个随机性 如果对clock机制进行一定的改造， 把1和0的bit标识改成数值(被引用次数)， 然后当一个缓存页码，每次访问的时候， 它对应的数值就会+1， 淘汰指针转动的时候则-1, 如果是0就该页就会被淘汰， 那么它就被改造成了类似LFU的模式

数据库日志

我们在前面的Buffer management的时候提到过淘汰缓存页时，就需要将数据写入磁盘， 为了保证数据的一致性， 需要用到WAL。WAL本质上是一种日志， 在某些数据库还会按照功能区分为： redo日志， undo日志， 简单来讲redo是为了数据恢复的， undo是为了将已经保存到了数据库的数据撤回的。 然后日志的类型会有两种， 一种是物理日志(pysical log)， 日志文件将会将数据直接记录在日志中； 另一种是逻辑日志(logical log)， 逻辑日志只记录了操作而没有数据。因为物理日志有数据， 所以通常会被用在redo阶段， 这样数据恢复会更快， 逻辑日志则会被用在undo阶段 这里我们说之所以会需要undo数据（写入了磁盘的数据并没有完成commit）， 写入磁盘的操作允许被发生在commit之后， 这种数据库策略通常被称为no-force/steal 策略，相对的force/no-steal则会要求数据在commit之前写入数据， 所以force策略下， 数据库在恢复的时候只要关心redo日志就好， 因为根据策略， 但凡是日志中显示commit是先需要写入磁盘的。 但是为啥数据库还会允许no-force的这种发生写盘操作在commit之后的操作存在呢， 原因也很简单， 提升tansaction的速度。 最后， 关于数据库日志还有一个概念是checkpoint， 顾名思义就是日志的记录点， 每个checkpoint都有一个对应的LSN（log sequence number, 单调增）， 目的是为了替身redo和undo效率的， 有了checkpont我自要从上一个LSN进行数据恢复操作就好了， 而不需要每次把所有脏页进行写盘

并发控制

数据库中由于并发引起的读写异常， 其实和隔离级别（isolation level）有关， 常见的隔离级别有(从低到高)：

• Read Uncomiited, 允许事务并发读取别的没有提交的事务， 这种隔离级别下， 很容易导致脏读
• Read Commited, 一个事务只能去读已经被提交了记录。但是这种隔离级别依然无法保证对相同数据同时读取（已经都是提交了的）， 能观察到相同的数据； 因为有可能在数据读取的过程中， 数据发生了改变， 导致并非读看到不一样结果
• Reapetable Read，所以在上一个隔离级别的基础上， 这个级别能保证 对数据的同时访问， 获取相同的结果
• Serializable， 最强的隔离级别， 意味着所有的事务都是按照时序展开， 会有最强的数据一致性保证，也就意味着最糟糕的并发性能

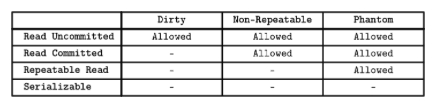
下图展示了各种隔离级别对应的读写异常的可能性， 可以看到Seriaizable基本是绝缘所有并发引起的读写异常， 当然代价就是牺牲并发.

3种并发控制流派

有三种常见的并发控制流派：

• OCC， Optimistic concurrency control
• MVCC, Multiversion concurency control
• PCC, Pessimistic concurency control

OCC

把事务分成三个阶段：

• Read phase
• Validation phase
• Write phase

在第一阶段， 会把所有并发的事务的dependency写入到read set（不改变数据库状态的操作）和write set中（会有副作用， 会改变数据库操作） 第二阶段， 就是根据read set和write set中的操作， 特别是有相交（冲突）部分的操作， 对那些可能会受影响的事务， 比如一个读相关的事务， 它的数据正在被另一个事务写， 那么这个读的事务就会被终止， 不然会导致脏读 第三阶段， 当然， 如果在第二阶段中没有检查到冲突，就可以顺利的提交

MVCC

简单来讲就是给所有的事务一个单调增的事务ID， MVCC通常不会阻止你去取旧的数据， 但是通常会确保在系统里面只存在一个没有提交的事务版本（version）

所以这种方式应该会产生脏读， 但是因为只允许耽搁未提交事务版本， 所以最终一致性还是可以保证的

PCC

PCC通常会和锁一起出现， 当然也有不需要要锁的实现方式， 其中最简单的PCC实现方式就是基于时间戳， 通常会有两个时间戳：

• max_read_timestamp
• max_write_timestamp

除了写操作被允许可以在max_write_timestamp之前被执行， 其他的操作不能在另一个读写操作的最大timestamp执行 相对而言， 基于锁的实现方式会更加流行

锁

死锁Deadlock

死锁会发生在两个进程或者说事务都在等待彼此去释放锁， 有点类似于循环引用的问题(A模块要导入b， b模块也要导入A)

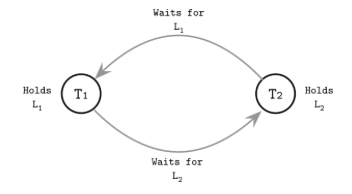怎么去解决死锁呢， 当然一种简单的方式就是给登台加上一个timeout时间， 这样就可以避免陷入无限等待。 还有方式就是让系统去识别这种可能造成死锁的状态， 也就是一个后台程序去检查事务直接存在不存在上面的waits-for graph， 如果存在就停掉其中的一个事务。

Latches

Latch也是锁， 但是和lock不一样的点在于， lock更多的是一种更高高级的抽象概念，远离数据库内核的存储结构。 而latch， 则是更接近数据存储结构的， 它是用来解决Page层面也就是更底层的竞争问题的。 我们可你是不希望一个Page在被更高或者说要被split和merge的时候被访问， 因为这样很可能会导致我们前面提到的读异常， 所以需要Latch在更底层帮我们去控制竞争。 但是由于B树的特殊性， 我们知道子节点的merge和split很有可能会向上传播到root（当然只是可能， 并不是绝对）， 那么仅仅在某个页面上进行竞争控制是不够的。一种相对朴素的实现方法， 就是对整个访问路径上的所有Page加上Latch, 淡然这种肯定胡牺牲性能。 所以更常用的方式， 是使用Latch crabbing的一种方式：这种方式它不会一直保留整个访问路径上的page上的锁， 而是从根节点开始， 不断向下， 只要当前节点不是full的状态(意味着大概率不会被至下而上的split merge影响） 我们就打开这个锁， 所以在特点的时间节点， Latch crabing只会给很小一部分page加锁

第六章 B-Tree Variants

如何提升基于B-Tree存储结构的数据库读写效率呢， 主要的改进方向其实就是->减少访问硬盘的次数和时间（特别是减少小批量的写入）, 再这种所提到的所有改进方法都是围绕这个核心点来的

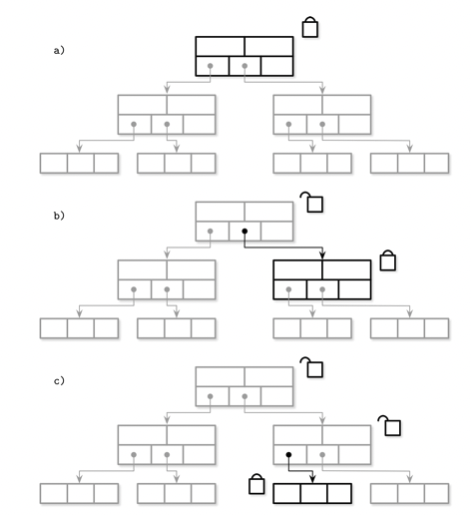
Copy-on-write B-Tree

传统的B-树， 一般底层使用latch来解决再并发时的问题， copy-on-write直接舍弃了这种方式，直接复制会被修改的page(也就是脏页)，同时不会阻止用户访问旧数据。 当新的Page结构被构建完成的时候， 更新原有B-Tree的指针， 指向新的Page即可:

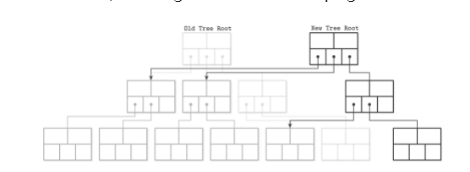
这种方式无疑是增加了磁盘空间的消耗， 好处有:

• 避免了latch的使用
• 读写互不影响
• 数据库系统也不会处在一种被污染的状态(无非就是新的页的pointer没有替换掉老的， 但是原来的树结构和数据还是完整的， 只是过时了而已)

Lazy B-Trees

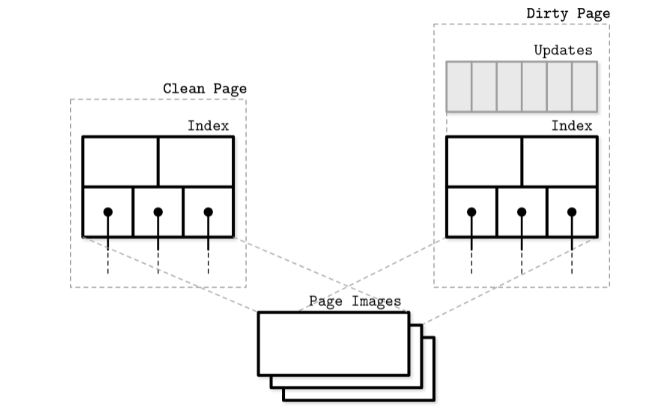
lazy B-Tree主要时通过结合内存或者说优化page cache的方式， 减少磁盘访问。以mongodb种使用的默认存储引擎WiredTiger为例（简称WT） WT首先会保留一份磁盘种的树结构， 当然只是Index， 并没有具体的数据。当某个page首次被读取的时候，这个page的内容会复制到到对应的update buffers， 用户可以被允许直接访问update buffers中的数据（还没被写入磁盘）， 后天程序会周期性地将update buffer数据写入到磁盘取覆盖原来的Page， 如果覆盖页的size大于原来的size， 它会拆分成多个页

FD-Tree

FD-Tree结合了B+tree和LSM树的特征（核心特点就是从随机磁盘写入->顺序写入）。 它在最顶层（也称为L0）会维护一颗树， L0在无法存储更多key的时候， 会把key融合到下一层（不是所有key， 而是特殊的key， 也被称为fence, 这些fence会有一个指向下一层的Pointer
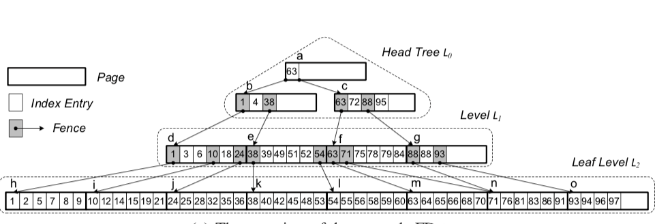
上图是FD-Tree的一个样例，可以看到最的顶层（L0）是一个树结构， 然后灰色的方框就是特殊的Index entry， 指向下一level的array的相同entry, 但是fence也有开那个中类型， 一种是external， 这种类型会被merge到下一层（也就是下一层会有一个相同的entry）， 另外一种是internal（比如上面的88）， 你会发现它只出现在L1没有出现在L2. FD-Tree的查找复杂度也是Log数量级

第七章

前面一章， 对数据库优化方向主要围绕减少磁盘写入开销的来的， 以WiredTiger为例的方法， 都是通过数据的缓存管理来实现上面这目标， 还有一种优化的方向， 就是把耗时的磁盘随机写入操作转化为磁盘的顺序写入， LSM-Tree就是这种思想的集大成者。 LSM-Tree， 全称log structed merge， 这个名字本身就昭示了这种存储结构的特征：

• log structure： 像日志一样只会在磁盘中追加写入(append only)
• merge， 不在磁盘中删改数据， 通过merge来应对不同版本数据的问题

LSM树由于append only的特征， 所以这种结构是非常适合写多于读的场景（吞吐量ingestion较高的场景）， 另外由于读写在结构上互不影响， 所以不会受类似B-tree的锁机制影响并发性能

LSM的构成

• Memtable(下面两个都算是memetable, 前者接受写， 后者只接受读）， 在内存中
• Current memtable
• Fushing memtable
• On-disk flush target
• Flush tables
• Compacting tables
• Compated tabe

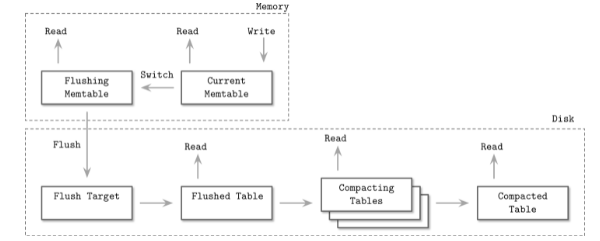
上图显示了LSM的整个生命周期，其中除了Current Memtable同时支持读写以外， 其他的阶段只支持读数据， 不支持数据的写入 另外有两个要点：

• 数据在内存中的时候， 它是排过序的
• 数据在被写入磁盘的时候， 也会用的WAL， 防止数据丢失
• 当数据被写入磁盘之后， 内存中的数据就会消失， 那么后续相关数据的查询之恶能通过磁盘中的数据获取

LSM中的更新和删除

更新的话很简单， 只要写入新的数据就好， 新的数据会在后买你覆盖旧数据，问题在于如何删除数据。由于我们不会直接删除LSM存储在磁盘的数据， 如果一个数据同时存储在Memtable和Disk table的情况下， 我如何在不直接删除Disk table的数据来实现删除呢。 常用的方法就是为这个需要被删除的key设置一个tomestone（墓碑）， 这样在merge的时候，老的数据会被tomestone覆盖掉， 就达到了删除的效果

LSM中的merge操作

因为数据会被存储在多个磁盘区域， 很有可能多个disk table这间会有数据冲突的问题， 即它们都保有相同key的数据， 所以需要通过merge来解决冲突 整个流程划分为一下三个步骤：

• 从不同的迭代器(就是存储在不同区域的磁盘数据， 他们本身是sorted的， 所以可以支持iteration)依次获取数据
• 把这些候选值入队（优先队列，可以通过min heap小顶堆来实现)， 最小的那个值放入结果集
• 继续从被选择的迭代器中补充数据加入队列

重复上面的流程， 如果第二个流程遇到key相同的情况， 可以选择通过记录本身携带的timestampe来解决冲突

LSM中的压缩(compact)

常用的方法有Leveled compaction和Size-tiered 这里以Leveled 为例， 位于顶层(接近0)的table会将数据不断“下沉” 到下一个level（前提是当前的level放不下更多table了）， 这个过程会对key的范围重合的table进行融合

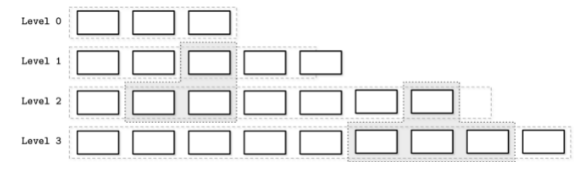
比如level 1 和 Level 2中的阴影部分， 它们key range 重合了， 所以需要融合。 融合的结果就是， 上面的数据， 也就是新的数据在观感上会一点点地“下沉”到下一个level。 另外， 通常来说下一层的Level会保留上一层2倍左右的大小

LSM的读/写/空间放大

我们优化数据的目标其实就是解决写放大， 读放大以及空间放大的问题：

• 读放大：需要读取多个地址来获取数据, LSM会有这个问题
• 写放大： 需要大量的重写操作， B树有这个问题， 在涉及到page层面的数据增删的时候， LSM的compact阶段其实也有
• 空间放大： LSM会有冗余数据， 所以这个很明显是有的

有一种指标RUM conjection（RUM分别代表read，update以及memeory）可以被用来比较及衡量一个数据库引擎的综合性能。我们需要了解的是， 通常来说， 解决上面中的任一一个问题， 都需要付出其他两个点中的1个或2个作为代价， 有点类似于分布式理论中的CAP理论， 你们很难同时拥有所有好处

LSM 实现细节

SSTable(sorted string table)

LSM树中的table是基于SSTable实现的

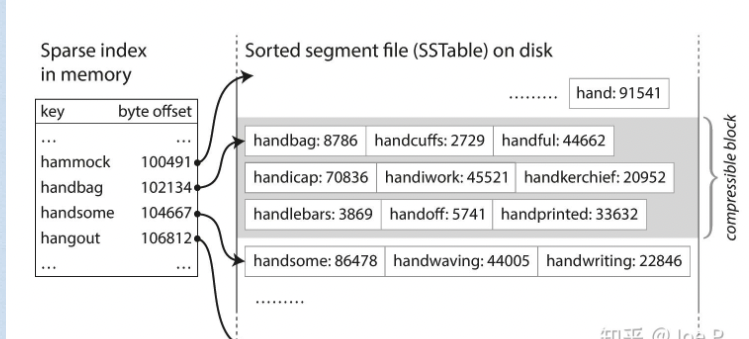
SST也会用到hash表， 但是是一个稀疏的hash表， 只记录了部分key和它们的位置（offset）， 数据本身是以key和value连续存储在磁盘上的

Bloom filter

LSM存在的一个性能瓶颈就是读放大， 就是它的数据存储在多个table， 如果存在一个key， 在所有的数据文件中并不存在， 它依然需要取读所有的文件， 从而成为性能瓶颈， 所以可以使用Bloom filter来过滤掉不存在的key， 今儿减少读放大引起的性能问题

Skiplist

将文件顺序地存储在内存的一种方式就是使用skiplist

Unordered LSM Storage

一一般来说lsm的数据都是以有序地形式被存储的， 当然也有并不是有序形式存储的结构

Bitcask

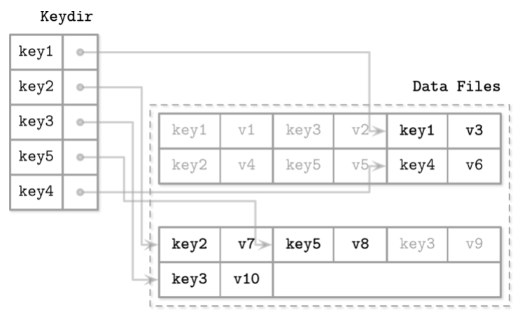
bitcask会在内存中保留一份key的最新路径的hash表(Keydir), keydir会在数据库初始话的时候被加载到内存， 所以很自然地会导致初始化时间过长的问题， 同时由于数据是直接被追加到磁盘的， 并不是有序（也没有什么memtable）， 所以bitcask也不支持范围查询（range query)。 但是它的优势也很明显， 首先点查询非常快， 同时写入数据是直接追加的所以写入性能也很好

Wisckey

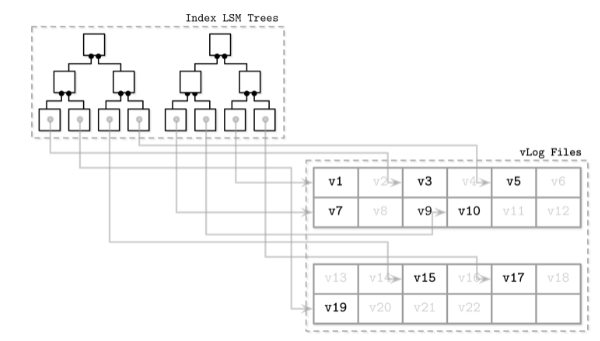
wisckey会将index和数据记录分开记录（SST， key和value是存储在一起的）， 分别存储在index lsm tree和vlog files。 vlogs files类似bitcask， 是无序地， 顺序增加的日志文件index lsm tree保留了指向vLog的指针， 所以它可以保留了范围查询的优点 它的缺点是， 有序vlog没有关于数据的l生命周期的信息(liveness, 也就是数据是不是仍然是有效的)， 所以在垃圾回收的时候， 必须要遍历左侧的index tree， 增加了复杂度。 传统的lsm， 哪怕是被删除的数据， 也可以在数据压缩阶段被直接覆盖(前面提到的类似墓碑的标记)